论文信息
- 论文名称:Joint Autoregressive and Hierarchical Priors for Learned Image Compression
- 论文作者:David Minnen, Johannes Ballé, George Toderici Google Research
- 发表时间:2018年、NIPS
前言与研究背景
在《Variational Image Compression With A Scale Hyperprior》(以下简称《Scale 2018》)提出基于超先验的熵建模方法后,Minnen 和 Ballé 在本篇论文中进一步拓展了这一思想。《Scale 2018》中所提的“scale”指的是对 latent 分布的标准差 σ 的建模,使得压缩模型能自适应不同区域内容的复杂度,提高压缩效率。
目前主流的学习型图像压缩方法普遍采用“变换编码”结构:首先用深度网络提取潜在表示(latent features),再通过熵编码对这些 latent 进行压缩,目标是让表示的熵尽可能低,从而达到更高压缩率。
论文指出,要提升压缩性能,关键在于提升熵模型对 latent 的概率分布估计能力。而这正依赖于对高斯分布的均值和方差建模是否准确。
我们可以把学习型图像压缩的发展分为如下几阶段:
Image Space(如 JPEG、BPG) → Latent Space(Ballé 2017) → Entropy Model(Ballé 2018) → Context Model(Minnen 2018)
值得注意的是,虽然“上下文模型”通常被认为是独立模块,但实质上它的引入也是为了增强熵模型的预测能力,从而进一步压缩码率。本文正是在这一方向上做出了新尝试。
目标函数与训练机制
学习型图像压缩的优化目标通常是最小化率失真损失函数:
$$
\mathcal{L} = R + \lambda \cdot D
$$
其中:
- $R$:表示压缩后的比特数;
- $D$:表示图像重建误差(如 MSE 或 MS-SSIM);
- $\lambda$:拉格朗日乘子,控制两者的权重平衡。
展开来看就是:
$$
R + \lambda \cdot D = \left[ -\log_2 p_{\hat{y}}(\lfloor f(x) \rceil) \right] + \lambda \cdot \left[ d\left(x, g(\lfloor f(x) \rceil) \right) \right]
$$
其中 $ f(x) $是编码器,$ f( \cdot ) $是解码器。量化符号 $\lfloor \cdot \rceil$ 实际训练中用加入均匀噪声模拟,从而保持端到端的可导性。损失函数中的第一个项,即负对数概率密度,直接用来估计码率,其误差通常在 1% 以内。
关于 MS-SSIM 做重建误差的疑惑
作者指出,当使用 MSE 作为失真度量时,训练目标等价于变分自编码器(VAE)。而使用 MS-SSIM 时,优化目标不再是概率意义上的似然函数,仅作为一个“感知”指标。
我疑惑的点是:为什么使用MS-SSIM指标的时候,作者认为他不是概率意义上的优化?在我看来,不管使用哪一种作为训练的重点,模型在反向传播梯度下降的时候都在优化均值和方差,这不还是对$\hat{y}$的概率分布优化吗?
本文之前的工作
在《Scale 2018》中,Ballé 首次提出通过引入 hyperprior z 来估计 latent y 的标准差 σ,使得不同图像区域(如边缘 vs 平滑区域)可以拥有不同的熵模型,从而提升整体压缩性能。
本篇文章进一步引入 高斯混合模型(GMM),不再只预测 σ,而是对均值 μ 和标准差 σ 同时建模,提升模型对 y 分布的表达能力。
此外,作者还引入了 自回归上下文建模(autoregressive context model),即通过已解码的 latent 元素 $ y_{<i} $ 来预测当前元素的分布。但这种方式无法并行,会带来解码速度上的牺牲。
为了弥补这一点,作者用超先验 z 提供全局信息,以补全上下文模型的局部预测不足,两者的 μ 和 σ 最终通过熵参数网络组合。
本文实现细节
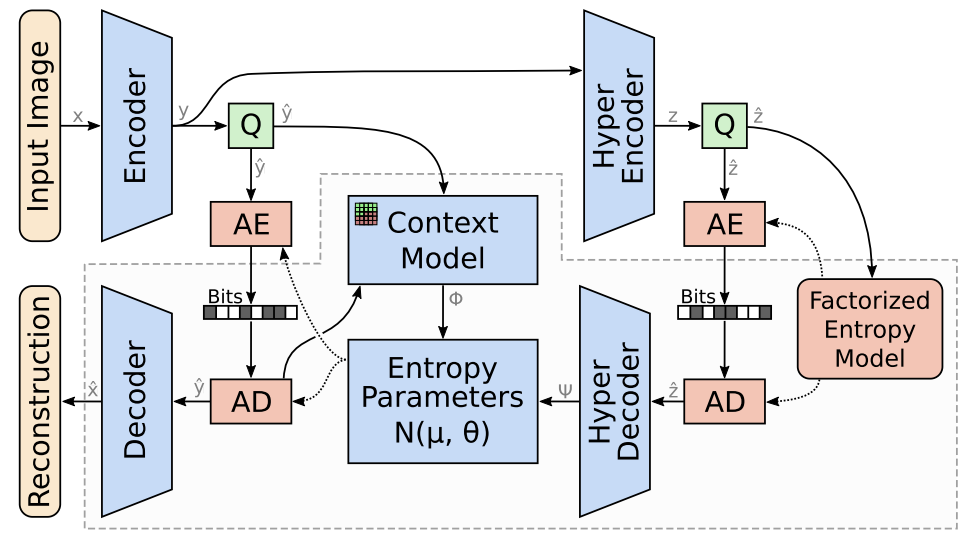
上图是作者提出的模型架构图,不难看出,Entropy Parameters Model 接收到来自 Context Model 和 Hyper Decoder 的信息后,会输出最终的 μ 和 σ。并将结果传递给算数编码器和算数解码器。

作者在这张图里交代了网络设计的细节
在模型结构设计中,编码器的最后一层是自编码器的瓶颈层,它的通道数决定了需要压缩的 latent 数量。虽然更少的通道有助于降低码率,但如果设得太小,特别是在目标码率较高时,会限制模型的表达能力,影响率失真性能。为此,作者采用了“通道冗余但可选择性使用”的策略:即使设置了较多的通道,模型可以通过输出恒定值并赋予其概率为1的方式“忽略”不重要的通道,这样这些通道不会增加实际的码率。
由于这种建模上的灵活性,作者将瓶颈通道数设得较大,然后让模型自己决定实际使用多少通道以获得最优压缩性能。这种策略在其实验结果章节中也有所体现。
在解码器部分,输出必须是RGB图像,因此最后一层固定为3个通道。而熵参数网络的输出需要预测每个 latent 的高斯分布的均值和标准差,因此其通道数必须是瓶颈通道数的2倍。上下文建模模块(Context Model)和超先验解码器(Hyper Decoder)没有通道数限制,但为了对齐实验,作者也将它们统一设置为瓶颈的2倍。
虽然理论上上下文模型可以使用所有已解码的 latent 来预测当前 latent 的参数,但在实际中,为了计算效率,作者只用了 5×5 的局部感受野,并通过掩码卷积(masked convolution)来防止信息泄露,做法类似 PixelCNN。而熵参数网络使用的是 1×1 卷积,仅对当前 latent 做预测,无法访问上下文模型中尚未预测的值。
作者还修改了loss函数,因为先验信息 z 也需要被编进码流中,所以应该做整体的优化:
$$
R + \lambda \cdot D = \left[ -\log_2 p_{\hat{y}}(\hat{y}) \right] + \left[ -\log_2 p_{\hat{z}}(\hat{z}) \right] + \lambda \cdot \left|| x - \hat{x} \right||_2^2
$$
实验结果
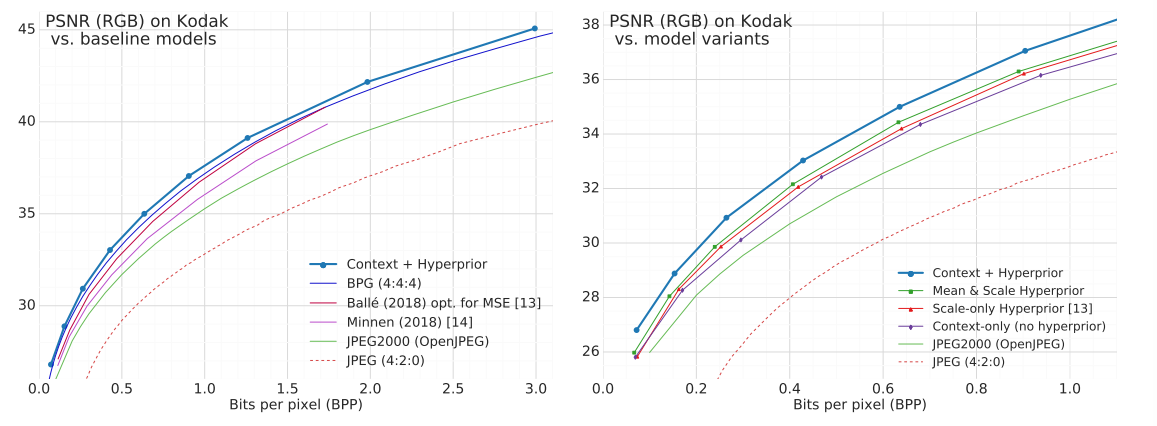
左边对比的试验结果表明,作者提出的方法优于当年所有的基于学习的压缩方法以及人工设计的BPG方式。右边的消融实验表明,引入上下文模型和超先验解码器可以进一步提升压缩性能。

如上图,作者还展示了一些可视化的实验结果,可以看出左边三张图在差不多的压缩率下,明显能比JEPG格式得到更好的图像质量。虽然我肉眼上没看出作者和Ballé的Scale-only以及BPG的结果有什么区别,但是作者认为更好:”Note the aliasing in the fence in the scale-only version as well as a slight global color cast and blurriness in the yellow rope.“。不过单单从评价指标的数据上来说,作者的方法确实是略优于中间两张的。
在展示这张对比图时候,我注意到作者在原文中提到”Creating accurate comparisons is difficult since most compression methods do not have the ability to target a precise bit rate.“,创建准确的比较很困难,因为大多数压缩方法没有能力针对精确的比特率进行调整。这个说法很有趣,因为在老师推给我最新一篇发表在IEEE Transactions on Multimedia上的论文,就是针对单一模型的码率无法动态调整而做的工作。《RDVC: Efficient Deep Video Compression with Regulable Rate and Complexity Optimization》后面几天会针对这篇论文进行精读。
读后总结
本文以 Ballé 的熵建模框架为基础,引入高斯混合模型与上下文信息,实现了对 μ 和 σ 的联合建模,提升了 latent 编码的表达能力;
结合上下文模型与超先验,使得模型既有局部预测能力,也有全局调控能力;
使用均匀噪声模拟量化,保留训练可导性;
通道数的冗余设定与压缩率之间并非单调关系,通过“无效通道抑制”提升了模型的实际表现。
这篇论文的技术设计为我们在学习视频压缩、上下文建模以及通道控制时提供了良好参考。后续如将本文思想延展到视频压缩(如 RDVC)中,还可以研究更细粒度的时空建模策略与复杂度自适应模块。