论文信息
论文名称:Learned Image Compression with Discretized Gaussian Mixture Likelihoods and Attention Modules
作者:Zhengxue Cheng, Heming Sun, Masaru Takeuchi, Jiro Katto
发表时间:2020,CVPR
前沿与研究背景
从前面的文章,我们可以得知Ballé做出了高斯scale混合模型(标准差),Minnen在此基础上完善做出了高斯混合模型(标准差和均值)。但是他们都是默认latent的分布为一个单一的高斯分布。
本文是在先前基于学习的图像压缩模型基础上的进一步探索,作者从两个方面出发以提升学习型图像压缩模型的表现:
引入离散高斯混合模型(Discretized Gaussian Mixture Model, DGMM)来建模 latent 表征的概率分布,取代传统的单一高斯分布,使熵建模能力更强;
在主干网络中集成注意力模块(Attention Module),提升特征提取和重建能力。
值得注意的是,本文并没有完全改写压缩模型的整体框架,而是在 Entropy Model 和主干网络两个关键位置做了增强改进,使其更贴近实际压缩场景下的性能需求。
相比传统的超先验模型,该论文的创新点主要是:
使用多高斯成分(Mixture)进行柔性建模;
将注意力机制引入编码器与解码器中;
实验结果首次在 Kodak、CLIC、DIV2K 多数据集上超过最新标准 HEVC/H.265 Intra 编码。
目标函数与训练机制
目标函数的形式与之前的基于学习的图像压缩模型相同,即:
$$
\mathcal{L} = R + \lambda \cdot D
$$
作者在本文中微调了loss函数的设计,因为引入了超先验信息 z,这与之前的带超先验信息的论文一致:
$$
\mathcal{L} = \mathcal{R}(\hat{y}) + \mathcal{R}(\hat{z}) + \lambda \cdot \mathcal{D}(x, \hat{x}) =
$$
$$
\mathbb{E} \left[ - \log_2 \left(p_{\hat{y}|\hat{z}}(\hat{y}|\hat{z}) \right) \right] + \mathbb{E} \left[ - \log_2 \left(p_{\hat{z}|\psi}(\hat{z}|\psi) \right) \right] + \lambda \cdot\mathcal{D}(x, \hat{x})
$$
注意由于没有关于$\hat{z}$的先验分布,作者使用了一个分解的密度模型 ψ 来对其建模和编码:
$$
p_{\hat{z}|\psi}(\hat{z}|\psi) = \prod_i \left( p_{\hat{z}_i|\psi}(\psi) * \mathcal{U}\left(-\frac{1}{2}, \frac{1}{2}\right) \right)(\hat{z}_i)
$$
- 卷积 ∗:表示对这两个分布做混合;
对所有的概率密度值做乘积,这样处理后可以估计出整体的 $p_{\hat{z}|\psi}$,用于熵编码(Entropy Coding)。
本文之前的工作
在《End-to-End 2017》中,Ballé 首次提出了将图片转化成 latent 表征的方法,即使用深度卷积神经网络(CNN)进行特征提取,再通过熵编码对这些 latent 进行压缩,巧妙的使用均匀噪声来模拟量化过程的同时保证训练过程使用的函数可导。
在《Scale 2018》中,Ballé 首次提出通过引入 hyperprior z 来估计 latent y 的标准差 σ,使得不同图像区域(如边缘 vs 平滑区域)可以拥有不同的熵模型,从而提升整体压缩性能。
在《Joint 2018》中,Minnen 进一步引入 高斯混合模型(GMM),不再只预测 σ,而是对均值 μ 和标准差 σ 同时建模,提升模型对 y 分布的表达能力。
在此基础上,Minnen还引入了自回归上下文建模(autoregressive context model),即通过已解码的 latent 元素 $ y_{<i} $ 来预测当前元素的分布。但这种方式无法并行,会带来解码速度上的牺牲。
然而,上述所有方法的估计分布与潜在表示的真实边际分布之间仍然存在差距。这代表着作者认为,模型没有很好的对 latent 的概率分布进行良好的建模,作者认为这是单峰高斯分布曲线表达能力有限导致的,所以作者提出了离散高斯混合模型(Discretized Gaussian Mixture Model, DGMM)。
本文实现细节
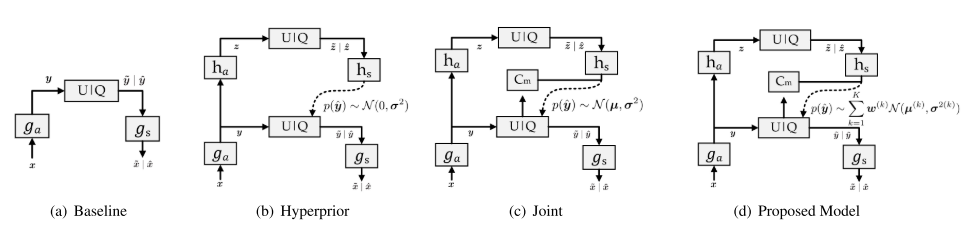
在详细讲解之前,我们来看一下作者在论文中展示的这张模型结构图,她从最开始的基于学习的图像压缩模型开始,逐渐扩展到本文的最终模型。这也是我们在上一篇文章中谈论过的学习型图像压缩发展经历的几个阶段。
(a)Baseline:这是一个最简单的基于学习的图像压缩模型。编码器和解码器都是深度卷积神经网络(CNN),用于提取和重建图像的特征。U|Q代表了量化和熵编码模块。
图像x输入到神经网络中,进行分析变换 $g_{a}$,把RGB图像变成一个连续的潜在表示 y。
这个 y 需要经过量化的过程,但是在真实量化后 y 会变成离散的值,这样不利于模型的训练,所以作者用均匀噪声进行模拟量化,得到$\tilde{y}$。
$\tilde{y}$表示经过了模拟量化后的潜在表示。再估计这个潜在表示的概率分布,得到$p_{\tilde{y}}(\tilde{y})$。
最后,使用算术编码对$\tilde{y}$进行编码,得到压缩后的比特流。
$g_{s}$代表合成变换,用潜在表示 y 重建出原始图像x。
(b)Hyperprior:在(a)的基础上引入了一个超先验变量 z,它是由潜在表示 y 通过另一个“辅助编码器”$h_{a}$得到的。这一步的目的是提取关于 y 的额外信息,用于帮助估计 y 的概率分布。
原始图像 x 经由编码器 $g_{a}$ 得到潜在表示 y;
y 经辅助编码器$h_{a}$提取出一个超先验 z,然后量化为 $\hat{z}$;
$\hat{z}$ 经由辅助解码器 $h_{s}$ 输出一个估计结果,用来预测 y 的标准差 σ;
用这个预测结果 σ 来构造一个高斯分布模型,进而完成 y 的概率建模;
…. 之后的流程和(a)没差了。
引入 z 后,模型在估计 y 的分布时更精确,有助于进一步降低码率。
(c)Joint:进一步在超先验的基础上,引入了上下文模型 $C_{m}$,用于更精细地建模 latent 表示。并且这里的超先验 z 不仅可以预测 y 的标准差 σ,还可以预测 y 的均值 μ。
… 前面流程和(b)差不多,不再不重复了。特别注意:超先验 z 可以预测 y 的 标准差 σ 和 均值 μ (此时并不准确)。
使用上下文模型 $C_{m}$分析已知的上下文(即 $y_{<i}$,已解码的latent的标准差和均值)对当前 latent 元素的影响;
将来自 $C_{m}$ 和 $h_{s}$ 的信息融合,获得当前 $\hat{y}$ 的精确分布(相对精确的 σ 和 μ)。
…
这种方法利用了局部上下文 + 全局超先验的联合建模策略,在不改变结构复杂度太多的情况下,显著提升了概率建模的准确性。
(d)Proposed Model:作者在(c)的联合建模基础上,将简单高斯分布升级为离散高斯混合分布(DGMM),进一步增强了模型表达能力。
前面流程和(c)差不多,首先从 𝑥 得到 𝑦,再得到 $\hat{z}$。
这次不再只是预测一个均值和方差,而是预测多个高斯分布分量的参数:多个 𝜇 和 σ,以及混合的权重 ω。
当前的 y 的概率分布被建模为一个加权的高斯混合:
$$
p(\hat{y}_i) =
$$
$$
\sum_{k=1}^{K} \omega^{(k)} \cdot \mathcal{N}(\mu^{(k)}, \sigma^{(k)})
$$
这种方式显著提升了模型对多模态 latent 分布的拟合能力,特别适用于复杂图像内容的压缩(如边缘、纹理、反射等区域)。
离散高斯混合似然
作者提出使用离散化的高斯混合模型(DGMM)来建模$\hat{y}$的概率分布:
$$
p(\hat{y}_i \mid \hat{z}) =
$$
$$
\left( \sum_{k=1}^{K} \omega_i^{(k)} \cdot \mathcal{N}(\mu_i^{(k)}, (\sigma_i^{(k)})^2) \right) * U\left(-\frac{1}{2}, \frac{1}{2}\right)(\hat{y}_i)
$$
作者采用 K=3 个混合分量,DGMM 可以自动为不同区域选择最合适的分布形状。如果是平滑区域,三个均值趋于一致,近似退化为单峰高斯,而当面对复杂边界的时候三个均值相距较远,表现出多峰特性。
每个像素点的权重、均值、方差都是可学习的,因此模型具有很强的自适应能力;
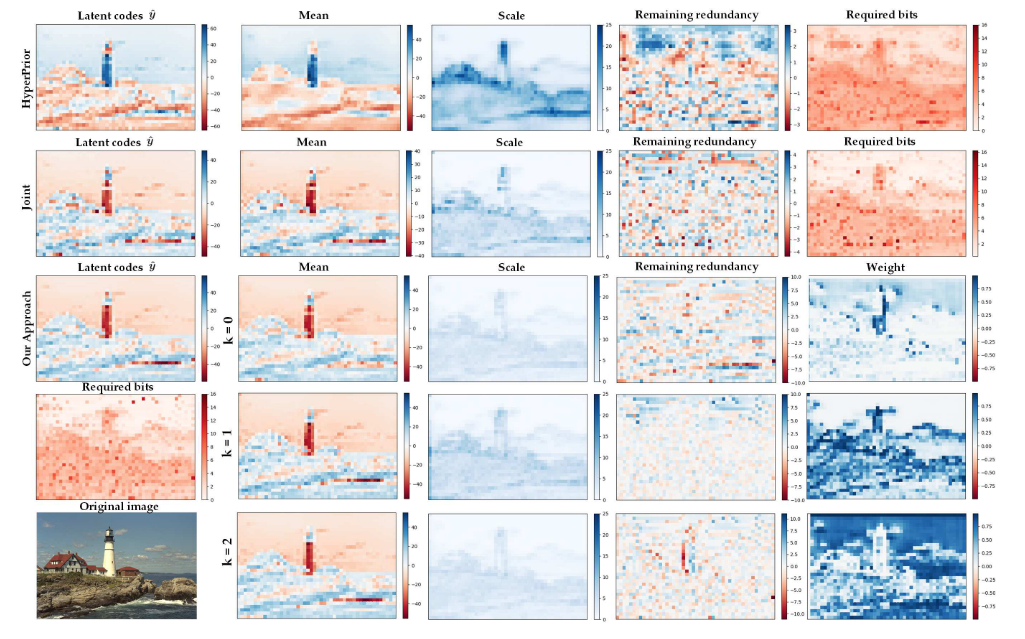
从上面的这张对比图我们可以看出,作者可视化的展现了不同模型之间的差异,从列顺序由左到右分别是:模型压缩前的潜在特征分布(原始特征),预测的高斯分布均值 𝜇,预测的标准差 𝜎,归一化残差 $(\hat{y}−μ)/σ$,表示熵模型未能捕捉的残余结构,实际编码每个位置所需比特数,Weight仅针对本文模型,表示每个混合高斯分量对每个像素位置的权重。
结果表明本文提出的离散高斯混合模型(DGMM)相比 Hyperprior 和 Joint 模型具有更好的空间建模能力和压缩性能。它能以更小的 scale、更少的比特、更少的冗余实现更精准的概率分布预测,这在天空、边缘、复杂区域中尤为明显。
同时你可以观察到在不同的层次,每个混合高斯分量分配的权重也有区别,这表明模型对不同区域的复杂度有不同的感知和响应。表明作者的工作是有所成效的。
注意力模块的改动
除了提出 DGMM 外还提出改进注意力模块的结构来优化模型,加快模型的训练成本。
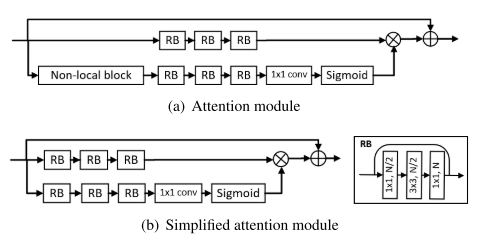
从图中我们可以观察到作者去除了 Non-local block 这个模块,作者认为完整的注意力模块训练代价高,移除了这个非局部模块后可以加快模型的训练过程。
同时作者在之前已经为了扩大感受野,在网络中引入了大量的残差块,所以去掉该模块后,模型依然能很好的观察到图像得到细节。
作者对比了原始和简化的注意模块在训练16个epoch所用的训练时间以及损失对比。实验表明,简化后的注意力模块不仅能显著降低训练损失,同时保持较低的计算开销。
| Module | (a) w/ NLB | (b) w/o NLB | w/o attention |
|---|---|---|---|
| Loss | 2.705 | 2.754 | 3.026 |
| Time(s)/epoch | 1119 | 336 | 216 |
实验结果
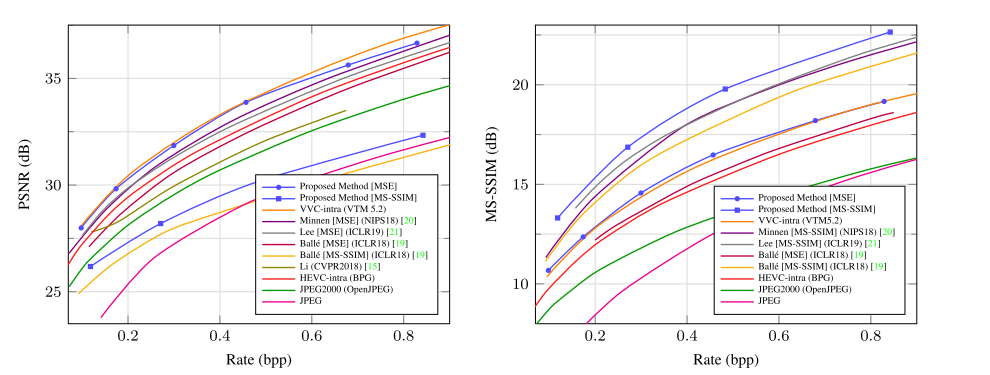
上图是作者的模型与其他手工设计以及其他学习型的模型在柯达数据集上的表现对比。可以看出在MS-SSIM指标上,作者提出的方法领先了起亚方法许多,但是在PSRN上只能和VVC的表现持平。总的来说还是取得了较为明显效果的,从人眼的观察角度来说能够提供更好的表现。
作者还用 CLIC 的高分辨率图片进行了测试,结果与上图差不多,在此就不多做展示了,都是在PSRN上表现略差于VVC,尤其是当bpp值上升的时候两者的区别愈加明显。


从作者展示的真实图像压缩效果来看,在相似的压缩率下,作者使用的方法确实要比其他的方法视觉效果好上很多,第一张图的窗子接缝处的边界十分清晰,但是哪怕是在PSNR值上表现优于本方法的VVC上,也依旧糊的很厉害。
读后总结
本文在现有学习型图像压缩框架的基础上提出了两个关键改进:一是采用离散高斯混合模型(Discretized Gaussian Mixture Model, DGMM)来建模潜在表示的分布,替代传统的单高斯模型,从而显著提升了熵建模的精度;二是设计了一个简化版的注意力模块,以低计算代价增强网络对图像结构复杂区域的感知能力。
在熵建模方面,DGMM 通过为每个 latent 元素预测多个高斯分量(均值、方差和权重),能够灵活适配不同区域的统计特征。例如,在平滑区域,多个分量会收敛为相似均值,近似为单峰高斯;而在复杂边界区域,则能展现出多峰概率,有效减少残余冗余。实验也验证了这种模型在空间结构表达上的优势,显著降低了编码所需比特数。
在网络结构方面,作者基于深残差结构,搭配子像素上采样单元和简化注意力模块,实现了感受野与性能的兼顾。特别是在注意力模块上,作者去除了代价昂贵的 non-local block,而仅保留关键机制,既提升了模型对困难区域的关注能力,也保证了训练效率,最终在多个数据集(如 Kodak)上表现优于现有方法。
整体来看,本文的工作为学习型图像压缩提供了更强的概率建模能力和更合理的结构设计思路。本文提出的这些方法,个人认为也可以推广到视频压缩上进行进一步的研究。